2.6. Solving the many-body problem¶
Note
The examples in this section take several minutes on a single core desktop computer. To speed up the computation the example scrips can be run in parallel, see section Parallelization with MPI.
We like to study manybody problem for an infinite one-dimensional chain. In second quantization the Hamiltonian reads
where \(\gamma_{ii} = 1\) and \(\gamma_{ij} = -1\) and \(w(t)\) is taken similar to section Solving one-body problems as
We are interested in the time evolution of the electron density
The time-dependent pulse \(w(t)\) which act on all lattice sites to the left of \(i_b\) is taken into account by a gauge transform similar to Time-dependent potentials and pulses and translates to a time-dependent coupling between \(i_b\) and \(i_b+1\). The Kwant code to build the system is
import kwant
import cmath
from scipy.special import erf
def gaussian(time, t0=40, A=1.57, sigma=24):
return A * (1 + erf((time - t0) / sigma))
# time dependent coupling with gaussian pulse
def coupling_nn(site1, site2, time):
return - cmath.exp(- 1j * gaussian(time))
def make_system(L=400):
# system building
lat = kwant.lattice.square(a=1, norbs=1)
syst = kwant.Builder()
# central scattering region
syst[(lat(x, 0) for x in range(L))] = 1
syst[lat.neighbors()] = -1
# time dependent coupling between two sites in the center
syst[lat(L // 2, 0), lat(L // 2 - 1, 0)] = coupling_nn
# add leads
sym = kwant.TranslationalSymmetry((-1, 0))
lead_left = kwant.Builder(sym)
lead_left[lat(0, 0)] = 1
lead_left[lat.neighbors()] = -1
syst.attach_lead(lead_left)
syst.attach_lead(lead_left.reversed())
return syst
Note that the code to build the system is basically the same as in the previous examples of the onebody problem which were treated in first quantization. The system looks similar to

For representation purpose, the central scattering system has been shrinked to only 20 sites in the plot and the time-dependent coupling is highlighed in red.
Two approaches are possible to obtain the density exectation value:
Either a high-level approach using manybody.State where the preprocessing is done
automatically and which provides additional functionality.
Alternatively a low-level approach
using manybody.WaveFunction, where the different preprocessing steps must be handled manually.
Both ways are shown below.
2.6.1. High-level automatic approach¶
The high-level approach comprises all preprocessing steps. The entire code is:
import tkwant
import kwant
import matplotlib.pyplot as plt
syst = make_system().finalized()
sites = [site.pos[0] for site in syst.sites]
times = [40, 80, 120, 160]
density_operator = kwant.operator.Density(syst)
state = tkwant.manybody.State(syst, max(times))
density0 = state.evaluate(density_operator)
for time in times:
state.evolve(time=time)
if time == 40:
state.refine_intervals()
error = state.estimate_error()
print('time={}, error={:10.4e}'.format(time, error))
density = state.evaluate(density_operator)
plt.plot(sites, density - density0, label='time={}'.format(time))
plt.legend()
plt.xlabel(r'site position $i$')
plt.ylabel(r'charge density $n$')
plt.show()
time=40, error=5.1438e-07
time=80, error=5.0540e-04
time=120, error=3.6453e-03
time=160, error=1.1463e-02
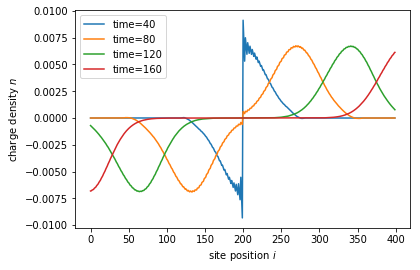
Note that this approach is much simpler and provides additional methods to fascilitate the numerical procedure without the need to fine-tune the quadrature by hand. While the high-level approach is less flexible, it can still be adapted in various ways. In the following we show how to change the lead occupation.
See also
The complete example script including MPI directives for parallel execution
can be found in
1d_wire_high_level.py.
Chemical potential and temperature of the leads¶
By default, the chemical potential and the temperature in all leads are identical and equal zero. To set them in all leads to the same, non-zero value, is possible via
occupations = tkwant.manybody.lead_occupation(chemical_potential=0.5, temperature=0.1)
state = tkwant.manybody.State(syst, max(times), occupations)
One can also set different values in each lead as
occup_left = tkwant.manybody.lead_occupation(chemical_potential=0.5, temperature=0.1)
occup_right = tkwant.manybody.lead_occupation(chemical_potential=0.2)
occupations = [occup_left, occup_right]
state = tkwant.manybody.State(syst, max(times), occupations)
Instead of a scalar value one can also provide a sequence of values for the chemical_potential,
one value for each band of the lead spectrum:
occupations = tkwant.manybody.lead_occupation(chemical_potential=[-0.5, 0.5])
In this case the number of values must match the number of bands in that lead.
The ordering of the bands in the same obtained with kwantSpectrum.
Adaptive refinement and error estimate¶
The class manybody.State provides methods to estimate the quadrature error
of the manybody integral and to adaptively refine the approximation to a given
accuracy.
The error ist estimated via
error = state.estimate_error()
print('estimated integration error= {:10.4e}'.format(error))
estimated integration error= 1.3478e-08
By default, the error is estimated on the density expectation value. One can obtain the error also for other expectation values, as e.g. the current:
current_operator = kwant.operator.Current(syst)
error = state.estimate_error(error_op=current_operator)
print('estimated integration error= {:10.4e}'.format(error))
estimated integration error= 6.7801e-10
The quadrature intervals can be refined via
state.refine_intervals();
By default, the refinement is done up to a certain accuracy of the density expectation value. Again, the behavior can be changed
current_operator = kwant.operator.Current(syst)
state.refine_intervals(rtol=1E-3, atol=1E-3, error_op=current_operator);
Note
Adaptive refinement is computationally expensive. Exploring initially at low precision is often a good idea.
2.6.2. Low-level manual approach¶
The low-level approach is close to the algorithm to solve the manybody problem which described in the Tkwant paper. The code is:
from tkwant import leads, manybody
import kwant
import kwantspectrum
import functools
import numpy as np
import matplotlib.pyplot as plt
syst = make_system().finalized()
sites = [site.pos[0] for site in syst.sites]
times = [40, 80, 120, 160]
density_operator = kwant.operator.Density(syst)
# calculate the spectrum E(k) for all leads
spectra = kwantspectrum.spectra(syst.leads)
# estimate the cutoff energy Ecut from T, \mu and f(E)
# All states are effectively empty above E_cut
occupations = manybody.lead_occupation(chemical_potential=0, temperature=0)
emin, emax = manybody.calc_energy_cutoffs(occupations)
# define boundary conditions
bdr = leads.automatic_boundary(spectra, tmax=max(times), emin=emin, emax=emax)
# calculate the k intervals for the quadrature
interval_type = functools.partial(manybody.Interval, order=20,
quadrature='gausslegendre')
intervals = manybody.calc_intervals(spectra, occupations, interval_type)
intervals = manybody.split_intervals(intervals, number_subintervals=10)
# calculate all onebody scattering states at t = 0
tasks = manybody.calc_tasks(intervals, spectra, occupations)
psi_init = manybody.calc_initial_state(syst, tasks, bdr)
# set up the manybody wave function
wave_function = manybody.WaveFunction(psi_init, tasks)
density0 = wave_function.evaluate(density_operator)
for time in times:
wave_function.evolve(time)
density = wave_function.evaluate(density_operator)
plt.plot(sites, density - density0, label='time={}'.format(time))
plt.legend()
plt.xlabel(r'site position $i$')
plt.ylabel(r'charge density $n$')
plt.show()
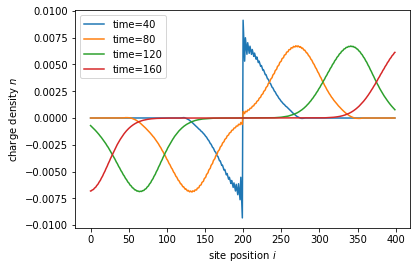
The role of each function can be deduced from the Tkwant paper and the function documentation. While most lines of above code are generic, a few lines are responsible for the numerical accuracy of the result and must be fine tuned for each problem in question.
The numerical accuracy is controled by the integration order (given by the variable order) of a quadrature interval
and by the number of sub intervals (by the variable number_subintervals), in which each initial quadrature interval is divided.
The actual value of the variable order, is less crucial and typically ranges
in between 10 and 20. The value of number_subintervals is highly system dependent and must be tuned.
Note
The numerical precision of the manybody expectation value is mainly determined
by the integer variable number_subintervals in above example.
Larger values lead to a more precise result on the cost of longer compute time.
The actual value is highly system dependent. It is a good practice to start
with a low value and to gradually increase it until the result converges.
To better understand the logic between these two parameters, let us state that
for Gaussian quadrature rules as Gauss-Legendre or Gauss-Kronrod,
the sampling points are not distributed equidistantly over the quadrature interval.
The purpose of the function manybody.split_intervals() is to split
a quadrature interval with a given order equidistantly into number_subintervals with similar order.
From this follows, that order=2 and number_subintervals=10 and
order=10 and number_subintervals=2 will both lead to the same number of sampling
points to approximate the integral, but with a very different distribution of the points.
See also
The complete example script including MPI directives for parallel execution
can be found in
1d_wire_low_level.py
2.6.3. Summary¶
To summarize, we like to highlight the similarity between the onebody and the
manybody approach.
The first one is the definition of the system using Kwant, which is the same,
whether the Hamiltonian is written in first quantization (onebody)
or in second quantization (manybody).
The second similarity is the API of the solvers for the onebody and the
manybody Schrödinger equation.
We will show this on the example of the two classes onebody.ScatteringStates() and
manybody.State().
After defining an observable, as e.g.
density_operator = kwant.operator.Density(syst)
both states can be evolved forward in time and evaluate expectation values similarly
Onebody
mode = 0
psi = tkwant.onebody.ScatteringStates(syst, energy=1, lead=0, tmax=10)[mode]
psi.evolve(time=5)
density = psi.evaluate(density_operator)
Manybody
state = tkwant.manybody.State(syst, tmax=10)
state.evolve(time=5)
density = state.evaluate(density_operator)
See also
More customization options for the high- and the low-level approach be found in the section Advanced manybody settings. Additional examples for solving the manybody Schrödinger equation can be found in the section More examples.
