2.12. Boundary conditions¶
To simulate open quantum systems with tkwant, modes that are propagating from a central scattering region into a lead are not supposed to return into the scattering region anymore. This behavior is ensured by special boundary conditions that we have to provide when solving the time-dependent Schödinger equation. No additional boundary conditions must be provided for closed systens, as the wavefunction is by definition zero at the system border.
The two high-level solver routines onebody.ScatteringStates() and
manybody.States() calculate internally the required boundary contitions.
This happens e.g. in the open system example
Evolution of a scattering state under a voltage pulse in a quantum dot,
when the solver is initialized:
psi = tkwant.onebody.ScatteringStates(syst, energy=1., lead=0, tmax=200)[0]
One can prevent the solver to use the internal default boundaries but pass own boundary conditions to the solver that will be used instead:
boundaries = tkwant.leads.automatic_boundary(syst.leads, tmax=200)
psi = tkwant.onebody.ScatteringStates(syst, energy=1., lead=0,
boundaries=boundaries)[0]
This is a good way to change default parameters and precalculating boundaries is also mandatory to
construct wave functions using the low level approach via onebody.WaveFunction().
We will show in this tutorial how boundary conditions work and how to calculate
and analyse them.
See also
An full example script showing how default boundaries are changed can be found in Alternative boundary conditions.
2.12.1. Basic formalism¶
We will use the approach developed in Ref. [1] employing an imaginary potential, to construct so-called absorbing boundary conditions. This tutorial will illustrate how to set absorbing boundary conditions in the general case. For advanced users, it also shows how to set up boundary conditions by hand and how to analyze them, if desired.
Absorbing boundary conditions are not ideal but have some spurious reflection. We define the reflection coefficient \(r\) by
The first term is the initial propagation of the plane wave \(\psi(x)\), whereas the second term is the reflected part. The reflection coefficient \(r\) ranges between zero (no reflection) and one (total reflection).
In the general case, different modes (indexed by \(\alpha\)) with corresponding wave vector \(k_{\alpha}\) are open for a given energy \(E\). We write the reflection as
To obtain the full lead reflection, we have to sum over all open modes:
2.12.2. A minimal example¶
We start with a simple example and construct boundary conditions for a
lead lead which is three sites wide.
The Hamiltonian of the system is
The system is translationally invariant in the direction of index i (which takes values from \(-\infty\) to \(\infty\)) and runs in j direction over the three sites 0, 1 and 2. Let us first construct the lead with kwant and show its spectrum with three bands in the first Brillouin zone.
import tkwant
import kwant
# create lead
def make_lead(W=3):
lat = kwant.lattice.square(a=1, norbs=1)
lead = kwant.Builder(kwant.TranslationalSymmetry((-1, 0)))
lead[(lat(0, y) for y in range(W))] = 2
lead[lat.neighbors()] = -1
return lead.finalized()
lead = make_lead()
kwant.plotter.bands(lead);
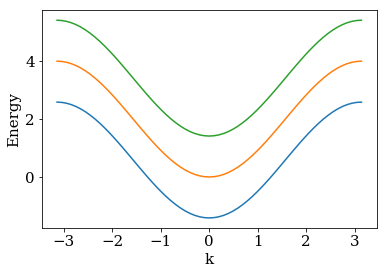
In a realistic model one has to imagine this lead attached to some central scattering
region that we like to study by a tkwant simulation. To make the
steps more explicit however, we will concentrate on the lead only in
this tutorial.
Automatic boundary conditions¶
The easiest way to construct boundary conditions is to use the fully
automatic routine automatic_boundary. We only have to provide the
lead and a maximal simulation time tmax, that we have to fix in
advance for the subsequent tkwant simulation.
boundary = tkwant.leads.automatic_boundary(lead, tmax=10000)
The boundary condition boundary is ready to use with the tkwant
solvers. It is intended to provide an optimal boundary for our system.
In the case that the system has several leads, one has to provide a sequence of
boundary condtions to the solver, a boundary condition per lead.
The automatic_boundary can take a sequence of leads as an input parameter
and returns automatically a sequence of boundaries, as in the initial example.
Changing default values¶
Without further arguments automatic_boundary,
the reflection r is smaller than a given default value. The value can be
changed by the keyword refl_max.
boundary = tkwant.leads.automatic_boundary(lead, tmax=10000, refl_max=1E-10)
If we have upper (like the Fermi energy for low temperatures) and or
lower energy cutoffs, we can pass it to the routine with the keyword
emax and emin. This might result in a computationally more
efficient boundary condition. If we simulate only modes between the
energies 0 and 1 we could write:
boundary = tkwant.leads.automatic_boundary(lead, tmax=10000, emin=0, emax=1)
WARNING:tkwant.leads:1321:rank=0: could not find maximal curvature value for spectrum within emin=0, emax=1
WARNING:tkwant.leads:1929:rank=0: problem to analyse spectrum for boundary conditions: unable to find max curvature point of the spectrum
This should be the standard way to construct boundary conditions that is
sufficient in most cases. If the algorithm in routine
automatic_boundary fails, or the performance of the obtained
boundary condition is too low and we like to optimize by hand, we
provide tools to set up and analyze boundary conditions by hand. They
are discussed in the two following paragraphs.
2.12.3. How do tkwant boundary conditions work¶
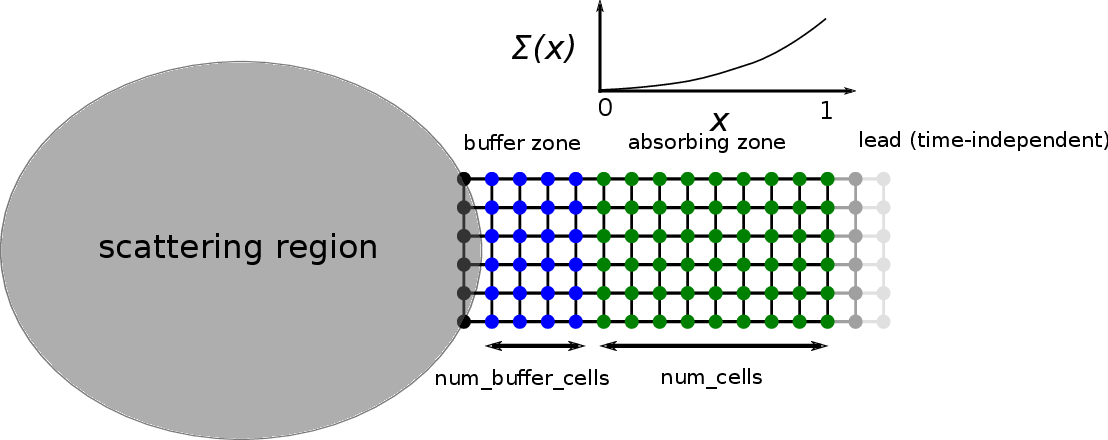
Technically, the tkwant boundary conditions work by additional cells,
that are inserted between the scattering region and the (time
independent) lead. Two different types of cells can be added. In the
buffer zone, which is the first zone connected to the scattering region
(colored in blue below), num_buffer_cells with the lead hamiltonian
are added. Here in our example, num_buffer_cells = 3 and the lead
width is 6. In the buffer zone, the modes coming from the system simply
continue to propagate into the lead during the simulation. A second zone
is the so-called absorbing zone (colored in green below), which is in
our example is num_absorb_cells = 9 cells long. An absorbing potential
\(i \Sigma(x)\) is added to the Hamiltonian in order to create
damping and absorb propagating waves. For convenience, we will often
skip the imaginary unit \(i\) in front of the absorbing potential
\(\Sigma(x)\). The first discrete absorbing cell corresponds to
\(x = 0\) of the (continous) argument for \(\Sigma(x)\), whereas
\(x = 1\) corresponds to the last absorbing cell on the right, that
is facing the time-independent lead (shown in grey). Having present only
buffer, absorbing, or both zones, we distinguish three types of boundary
conditions, that we discuss in the following.
Simple boundary conditions¶
One can also set up boundary conditions by hand. The simplest boundary
condition consists in adding num_buffer_cells additional cells that are
explicitly taken into account in the time-dependent simulation, in
between the scattering region and the lead. This type of boundary
conditions can be obtained via:
boundary = tkwant.leads.SimpleBoundary(num_buffer_cells=1000)
Up to the simulation time of 2 * num_buffer_cells / vmax
where vmax is the maximal velocity of a mode in the lead,
very little reflection is comming from the lead where this boundary is used.
The disadvantage of this type of boundary condition is that it is
becomes very inefficient for long simulation times, as the number of
added lead cells num_buffer_cells increases linearly with the maximal time
tmax.
Monomial absorbing boundary conditions¶
An often much better approach is to use absorbing boundary conditions,
that add an imaginary background potential \(\Sigma(x)\) onto the
num_absorb_cells additional lead cells, in order to absorb waves that are
propagating into the lead. The specific form of a monomial imaginary
potential
was explored in Ref. [1]. This boundary can easily set up by writing:
num_absorb_cells = 400
boundary = tkwant.leads.MonomialAbsorbingBoundary(num_absorb_cells, strength=10, degree=4)
where n is the degree of the polynomial and A corresponds to the
strength. The absorbing boundary condition has the advantage that no
maximal time has to be choosen in advance of the simulation. In
addition, it has a much better scaling behavior, as the number of
explicit lead cells num_absorb_cells does not scale linearly with the
simulation time as before. The disadvantage of this approach is that the
choice of the three parameters, as the one we took above, is rather
heuristic. As absorbing boundary conditions will always lead to a
hopefully small, but finite reflection from the lead, this is especially
unpleasant as we have no explicit control of the error in advance. We
will show in the later section however how to estimate the lead
reflection for a given choice of the parameters, respectivelly a generic
imaginary potential \(\Sigma(x)\).
As a side remark, let us state that the routine automatic_boundary
employs an algorithm to estimate an optimal choice of the monomial
parameters degree, strength and degree (and also additional
buffer cells num_buffer_cells, that will be discussed below), such
that the reflection stays below a given value refl_max. It then
returns either a MonomialAbsorbingBoundary or a SimpleBoundary
condition, depending on which one is computationally more efficient.
General absorbing boundary conditions¶
Finally, one may choose an arbitrary static imaginary potential
\(\Sigma(x)\) to construct an absorbing boundary condition. The
argument domain is \(0 \leq x \leq 1\). Having
num_total_cells = num_absorb_cells + num_buffer_cells lead
cells, \(x = 0\) corresponds to the first lead cell (index 0)
that is connected to the scattering region respectively to the buffer,
if num_buffer_cells > 0, whereas \(x = 1\) corresponds to the
the last lead cell (index num_total_cells - 1). The specific form of
monomial potential used above can be simply recovered by setting:
def my_imaginary_potential(x):
return 50 * x**4
boundary = tkwant.leads.GenericAbsorbingBoundary(num_absorb_cells, my_imaginary_potential)
2.12.4. Lead reflection analysis¶
Basic analysis¶
The most obvious way to study unintended reflections of an absorbing
lead is to perform the time dependent tkwant simulation with
different boundary conditions and check a posteriori the observables
afterwards for spurious reflections. Alternatively, as a tkwant
simulations are computationally demanding, one can perform an a priori
estimate of the lead reflection with an imaginary potential
\(\Sigma(x)\) by a static kwant calculation. The absorbing
potential can then be tuned to meet a desired maximal reflection.
The AbsorbingReflectionSolver calculates the reflection for an
absorbing lead of length num_absorb_cells with the imaginary potential
\(\Sigma(x)\). Calling an instance of AbsorbingReflectionSolver
for a given energy energies, it returns the reflection, momenta and
velocities of all open modes at this energy.
reflection_solver = tkwant.leads.AbsorbingReflectionSolver(lead, num_absorb_cells,
my_imaginary_potential)
refl, k, vel = reflection_solver(energies=0.5)
print('reflection = {}'.format(refl))
print('momenta = {}'.format(k))
print('velocities = {}'.format(vel))
reflection = [4.5107e-05 2.8341e-07]
momenta = [1.5279 0.7227]
velocities = [1.9982 1.3229]
Advanced analysis¶
As the number of open modes and also their ordering might change with
the energy, it becomes tedious to analyze a more complicated spectrum
with the AbsorbingReflectionSolver. A more convenient way is to use
the AnalyzeReflection class. Calling an instance of this class with
a momentum k and the band index band, we obtain the reflection,
energy and velocity of the corresponding mode
analyze_reflection = tkwant.leads.AnalyzeReflection(lead, num_absorb_cells,
my_imaginary_potential)
refl, energy, vel = analyze_reflection(k=0.2, band=1)
print('reflection = {:10.4e}, energy = {:6.4f}, velocity = {:6.4f}'.format(refl, energy, vel))
reflection = 2.8802e-08, energy = 0.0399, velocity = 0.3973
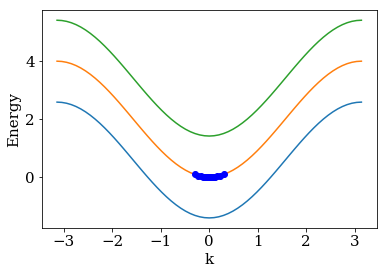
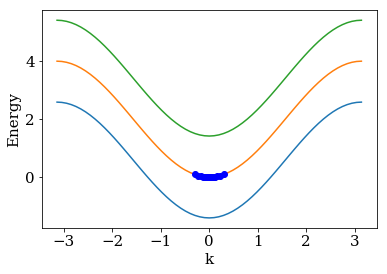
Moreover, we expect strong reflections around the local dispersion
minima or maxima. The around_extremum method of the
AnalyzeReflection provides an easy way to examine these regions.
Note that plots very similar to the one in Ref. [1]
can be obtained easily in this way.
In the figure, “relative energy” denotes \(E_{n=1}(k) - E_{n=1}(0)\).
The blue dots around the minima of
the middle band are the one for which we calculated the reflection.
import matplotlib.pyplot as plt
# helper routine for log plots
def log_plot(x, y, xlabel, ylabel=r'$r$', show=True):
plt.plot(x, y, 'o')
plt.xscale('log')
plt.yscale('log')
plt.xlabel(xlabel)
plt.ylabel(ylabel)
if show:
plt.show()
# reflection around dispersion minimum of band 1
refl, e, vel, k, e0, k0 = analyze_reflection.around_extremum(kmin=-0.3, kmax=0.3,
band=1)
log_plot(e, refl, xlabel='relative energy')
# lead dispersion and the location of the points for that we calculated the reflection
kwant.plotter.bands(lead, show=False)
plt.plot(k + k0, e + e0, 'ob')
plt.show()
0.0
-6.071532165918825e-18
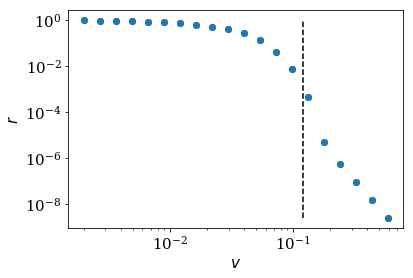
We can get rid of the slow modes with high reflection by adding an
additional buffer zone in between the scattering region and the
absorbing region. Adding num_buffer_cells to the lead and plotting
the reflection against the velocity, the modes with a velocity smaller than
buffer_vmax will not lead to reflection as they stay into the buffer
zone (the part on the left of the horizonal black dashed line in the
figure below). Only the modes with velocity higher than buffer_vmax will
be surpass the buffer zone and reflected in the absorbed region (the
part on the right of the horizonal black dashed line in the figure
below).
num_buffer_cells, tmax = 600, 10000
buffer_vmax = 2 * num_buffer_cells / tmax
plt.plot([buffer_vmax] * 2, [min(refl), max(refl)], 'k--')
log_plot(vel, refl, xlabel=r'$v$')
2.12.5. An advanced example with “nasty modes”¶
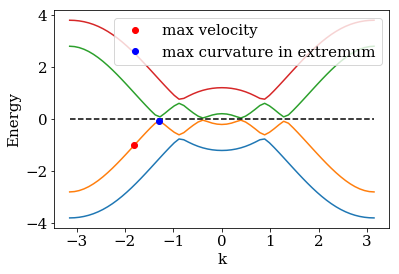
We will consider a more involved problem with hybidized bands. In contrast to the former simple problem, the small band gaps at the avoided crossings lead to pretty high curvatures in the local dispersion extrema. This means that we get fast modes with relatively low excitation energies, measured from the local extrema, such that these modes travel fast through the buffer but are also strongly reflected from the absorbing potential \(\Sigma(x)\).
We first plot the spectrum and also mark two modes that have different requirements for the monomial parameter optimization of the boundary algorithm:
One mode with high curvature and low excitation energy. The low energy
of this mode means that it is strongly reflected at the imaginary
potential, so the strenght parameter needs to be small. In contrast
to the former problem however, the low-energy mode propagates fast due
to the high curvature. It is therfore not cut off by the buffer zone as
in the previous example. A second mode with high velocity and high
excitation energy. This mode is not supposed to be captured by the
buffer zone, but needs a strong enough imaginary potential with a large
strength parameter to be well absorbed. The reflection at the
absorbing potential plays a much weaker role than for the low energy
mode.
import numpy as np
import tinyarray as ta
import kwantspectrum
# definition of the lead
def hybrid_lead(Delta=0.1, alpha=0.3, Ez=0.5, Ef=0.7):
s0 = [[1, 0], [0, 1]]
sx = [[0, 1], [1, 0]]
sy = [[0, -1j], [1j, 0]]
sz = [[1, 0], [0, -1]]
sz0 = ta.array(np.kron(sz, s0), complex)
szx = ta.array(np.kron(sz, sx), complex)
s0z = ta.array(np.kron(s0, sz), complex)
sx0 = ta.array(np.kron(sx, s0), complex)
def onsite_S(*x):
return (2 - Ef) * sz0 + Ez * s0z + Delta * sx0
def hopping(*x):
return -sz0 - 1j * alpha * szx
lat = kwant.lattice.square(norbs=4)
lead = kwant.Builder(kwant.TranslationalSymmetry((-1, 0)))
lead[lat(0, 0)] = onsite_S
lead[lat.neighbors()] = hopping
return lead
lead = hybrid_lead().finalized()
fermi_energy = 0
# plot the dispersion
spectrum = kwantspectrum.spectrum(lead)
k1, k2 = -1.80350, -1.29787
vmax = np.abs(spectrum(k1, band=1, derivative_order=1))
gmax = np.abs(spectrum(k2, band=1, derivative_order=2))
print('max velocity = {:6.4f}, max curvature = {:6.4f}'.format(vmax, gmax))
kwant.plotter.bands(lead, show=False)
plt.plot([-np.pi, np.pi], [fermi_energy] * 2, 'k--')
plt.plot(k1, spectrum(k1, band=1), 'or', label='max velocity')
plt.plot(k2, spectrum(k2, band=1), 'ob', label='max curvature in extremum')
plt.legend()
plt.show()
max velocity = 2.0436, max curvature = 42.5971
Estimate optimal monomial parameters¶
We can check the monomial parameters that automatic_boundary
proposes from the returned boundary instance:
boundary = tkwant.leads.automatic_boundary(lead, tmax, refl_max=1E-5,
emax=fermi_energy)
print('num_absorb_cells = {b.num_absorb_cells}, strength = {b.strength:6.4f}, '
'degree = {b.degree}, num_buffer_cells = {b.num_buffer_cells}'
.format(b=boundary[0]))
num_absorb_cells = 1861, strength = 109.0439, degree = 6, num_buffer_cells = 2126
Alternatively, we can call directly the parameter estimate routine, that
is internally used by automatic_boundary to obtain the monomial
parameters:
tmp = tkwant.leads._monomial_parameter_estimate(spectrum, tmax,refl_max=1E-5,
degree=6, emax=fermi_energy)
num_absorb_cells, strength, num_buffer_cells, *_ = tmp
print('num_absorb_cells = {}, strength = {:6.4f}, num_buffer_cells = {}'
.format(num_absorb_cells, strength, num_buffer_cells))
num_absorb_cells = 1861, strength = 109.0439, num_buffer_cells = 2126
Reflection of the nasty modes¶
As before, we can now analyze the refection of the lead with the
specific monomial potential. We will use however the
AnalyzeReflectionMonomial class, which has a similar functionality
as the AnalyzeReflection class, but which uses approximate
analytical expressions derived in Ref. [1] to estimate
the reflection. The AnalyzeReflectionMonomial class is much faster
than the AnalyzeReflection class.
Again, we plot the maximal buffer velocity buffer_vmax, meaning that
the modes with velocities on the left hand side of the black dashed line
are cut off by the buffer. We also plot the maximal reflectivity
refl_max that we required at the beginning by the grey dashed
horizontal line. Note that the reflectivity of all mode modes that are
not cut off by the buffer zone have a reflectivity smaller that value,
as required.
# analyze the reflection around two local extremas
analyze_reflection = tkwant.leads.AnalyzeReflectionMonomial(lead, num_absorb_cells,
strength, degree=6)
refl, e, vel, k, e0, k0 = analyze_reflection.around_extremum(kmin=-1, kmax=-0.7,
band=0)
plt.plot(vel[vel > 0], refl[vel > 0], 'o', label='band 0')
refl, _, vel, *_ = analyze_reflection.around_extremum(kmin=-1.6, kmax=-1, band=1)
plt.plot(-vel[vel < 0], refl[vel < 0], 'o', label='band 1')
# plot the buffer velocity cutoff
buffer_vmax = 2 * num_buffer_cells / tmax
plt.plot([buffer_vmax] * 2, [np.min(refl), np.max(refl)], 'k--',
label='buffer velocity')
# plot the maximal allowed reflection
plt.plot([np.min(vel[vel > 0]), np.max(vel[vel > 0])], [1E-5] * 2, 'k--',
alpha=0.4, label='required max. reflect.')
plt.xscale('log')
plt.yscale('log')
plt.xlabel(r'$v$')
plt.ylabel(r'$r$')
plt.legend()
plt.show()

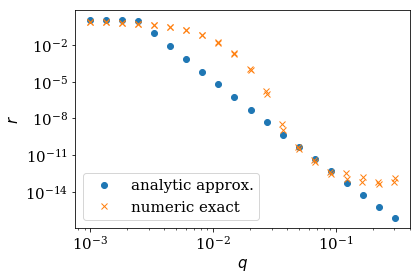
Comparison of the reflection from the numerical exact and the monominal approximation¶
Let us compare the approximate analytical expression (via
AnalyzeReflectionMonomial) with the numerical exact result from the
static kwant calculation (via AnalyzeReflection). Good agreement
with the exact numerical result can only be expected if
The length l corresponds to num_absorb_cells and the momentum q is the
distance from a local extremum \(k_0\) of the spectrum. We also plot
the time to show the interest of performing the analytical calculation,
even though it is only approximate.
import time as tt
# reflection from approximate analytical relation
start_time = tt.time()
analyze_reflection = tkwant.leads.AnalyzeReflectionMonomial(lead, num_absorb_cells,
strength, degree=6)
refl, e, vel, k, e0, k0 = analyze_reflection.around_extremum(kmin=-1.6, kmax=-1, band=1)
plt.plot(np.abs(k[vel > 0] - k0), refl[vel > 0], 'o', label='analytic approx.')
print('elapsed time monomial approximation: ', tt.time() - start_time)
# reflection from exact numerical kwant calculation
def my_imaginary_potential(x, degree=6):
return (degree + 1) * strength * x**degree
start_time = tt.time()
analyze_reflection = tkwant.leads.AnalyzeReflection(lead, num_absorb_cells,
my_imaginary_potential)
refl, e, vel, k, e0, k0 = analyze_reflection.around_extremum(kmin=-1.6, kmax=-1,
band=1)
plt.plot(np.abs(k[vel > 0] - k0), refl[vel > 0], 'x', label='numeric exact')
print('elapsed time exact numerical: ', tt.time() - start_time)
print('reflection around low-energy mode: energy= {:6.4f}, k0= {:6.4f}'.format(e0, k0))
plt.xscale('log')
plt.yscale('log')
plt.xlabel(r'$q$')
plt.ylabel(r'$r$')
plt.legend()
plt.show()
elapsed time monomial approximation: 0.2969198226928711
-1.2978741106509617
-0.07561865115991254
elapsed time exact numerical: 38.069809913635254
reflection around low-energy mode: energy= -0.0756, k0= -1.2979
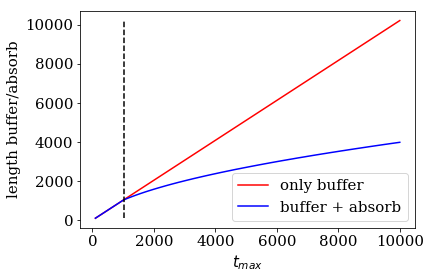
Comparison of the lead length for simple or absorbing boundary conditions¶
If the the maximal simulation time tmax is very small, we can
always cut of all modes by a buffer zone that is large enough to cut off
the fastest mode of the spectrum. We will therefore always find a trade
off between required reflection refl_max and tmax.
Let us plot the total length of the lead cells, that is the sum of
num_absorb_cells and buffer_cells, for different maximal simulation
times tmax, keeping refl_max fixed. Note that our parameter
estimate algorithm _monomial_parameter_estimate will use a sole
buffer zone as a fallback in the case that the absorbing boundary
conditions turn out to be disadvantageous. For for maximal simulation
times on the left hand side of the black dashed line, simple boundary
conditions perform better then absorbing boundary conditions, and vice
versa for maximal simulation times choosen on the right-hand side of the
back line. The automatic_boundary routine will therefore switch from
SimpleBoundary to MonomialAbsorbingBoundary if tmax
increses for refl_max.
def len_lead(tmax):
tmp = tkwant.leads._monomial_parameter_estimate(spectrum, tmax, refl_max=1E-5,
degree=6, emax=fermi_energy)
num_absorb_cells, _, num_buffer_cells, *_ = tmp
return num_absorb_cells + num_buffer_cells
times = np.linspace(100, tmax, 100)
buffer_len = [vmax * t / 2 for t in times]
absorb_len = [len_lead(t) for t in times]
plt.plot(times, buffer_len, 'r', label='only buffer')
plt.plot(times, absorb_len, 'b', label='buffer + absorb')
plt.plot([1037] * 2, [np.min(buffer_len), np.max(buffer_len)], 'k--')
plt.xlabel(r'$t_{max}$')
plt.ylabel(r'length buffer/absorb')
plt.legend()
plt.show()
2.12.6. References¶
[1] J. Weston and X. Waintal, Linear-scaling source-sink algorithm for simulating time-resolved quantum transport and superconductivity, Phys. Rev. B 93, 134506 (2016). [arXiv]
