Alternative boundary conditions¶
The physical system in this example is similar to Evolution of a scattering state under a voltage pulse in a quantum dot.
tkwant features highlighted
Selecting boundary conditions manually
Impact of the boundary type on performance
import time as timer
import numpy as np
from matplotlib import pyplot as plt
import kwant
import tkwant
def make_system(a=1, gamma=1.0, radius=10):
"""Make a tight binding system on a single square lattice"""
# `a` is the lattice constant and `gamma` the hopping integral
# both set by default to 1 for simplicity.
lat = kwant.lattice.square(a, norbs=1)
syst = kwant.Builder()
# Define the quantum dot
def circle(pos):
(x, y) = pos
return x ** 2 + y ** 2 < radius ** 2
syst[lat.shape(circle, (0, 0))] = 4 * gamma
syst[lat.neighbors()] = -gamma
lead = kwant.Builder(kwant.TranslationalSymmetry((-1, 0)))
lead[(lat(0, j) for j in range(-radius // 2 + 2, radius // 2 - 1))] = 4 * gamma
lead[lat.neighbors()] = -gamma
syst.attach_lead(lead)
syst.attach_lead(lead.reversed())
return syst
# for adding a time-dependent voltage on top of the leads
def faraday_flux(time):
return 0.05 * (time - 10 * np.sin(0.1 * time))
def evolve(times, psi, operator):
ops = []
for time in times:
psi.evolve(time)
expectation = psi.evaluate(operator)
ops.append(expectation)
return ops
def main():
syst = make_system()
# add a time-dependent voltage to lead 0 -- this is implemented
# by adding sites to the system at the interface with the lead and
# multiplying the hoppings to these sites by exp(-1j * faraday_flux(time))
extra_sites = tkwant.leads.add_voltage(syst, 0, faraday_flux)
lead_syst_hoppings = [(s, site) for site in extra_sites
for s in syst.neighbors(site)
if s not in extra_sites]
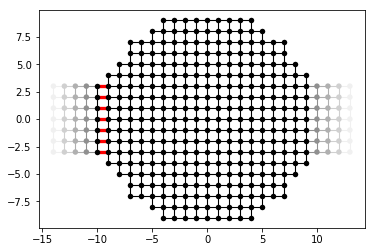
kwant.plot(syst, site_color='k', lead_color='grey', num_lead_cells=4,
hop_lw=lambda a, b: 0.3 if (a, b) in lead_syst_hoppings else 0.1,
hop_color=lambda a, b: 'r' if (a, b) in lead_syst_hoppings else 'k')
syst = syst.finalized()
# create an observable for calculating the current flowing from the left lead
current_operator = kwant.operator.Current(syst, where=lead_syst_hoppings,
sum=True)
energy = 1.
tmax = 600
# create initial scattering state
scattering_states = kwant.wave_function(syst, energy=energy, params={'time': 0})
psi_st = scattering_states(0)[0]
# maximal velocity of a mode in the leads
vmax = 2 * np.linalg.norm(syst.leads[0].inter_cell_hopping(), ord=2)
num_buffer_cells = int(vmax * tmax / 2)
# boundary conditions typically used by `tkwant.solve`
simple_boundaries = [tkwant.leads.SimpleBoundary(num_buffer_cells)
for l in syst.leads]
# boundary conditions with an absorbing potential that increases
# according to x**n where `x` is the distance into the lead
absorbing_boundaries = [tkwant.leads.MonomialAbsorbingBoundary(num_absorb_cells=100,
strength=10,
degree=6)
for l in syst.leads]
# create time-dependent wavefunctions that starts in a scattering state
# originating from the left lead, using two different types of boundary
# conditions
psi_simple = tkwant.onebody.WaveFunction.from_kwant(syst=syst, psi_init=psi_st,
boundaries=simple_boundaries,
energy=energy)
psi_alt = tkwant.onebody.WaveFunction.from_kwant(syst=syst, psi_init=psi_st,
boundaries=absorbing_boundaries,
energy=energy)
# evolve forward in time, calculating the current
times = np.arange(0, tmax)
# Simple boundary conditions
start = timer.process_time()
current_simple = evolve(times, psi_simple, current_operator)
stop = timer.process_time()
print('Simple Boundary conditions elapsed time: {:.2f}s'.format(stop - start))
# Absorbing boundary conditions
start = timer.process_time()
current_alt = evolve(times, psi_alt, current_operator)
stop = timer.process_time()
print('Absorbing Boundary conditions elapsed time: {:.2f}s'.format(stop - start))
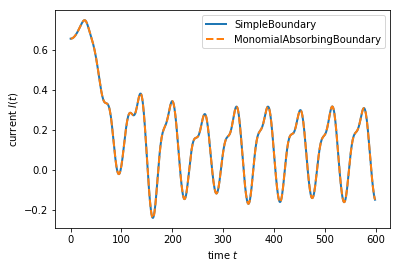
plt.plot(times, current_simple, lw=2, label='SimpleBoundary')
plt.plot(times, current_alt, '--', lw=2, label='MonomialAbsorbingBoundary')
plt.xlabel(r'time $t$')
plt.ylabel(r'current $I(t)$')
plt.legend()
plt.show()
if __name__ == '__main__':
main()
Simple Boundary conditions elapsed time: 3.58s
Absorbing Boundary conditions elapsed time: 2.05s
See also
The complete source code of this example can be found in
alternative_boundary_conditions.py.
