2.3. Second example: Fabry-Perot interferometer¶
We consider an infinite one-dimensional chain with nearest-neighbor hopping, in which two potential barriers A and B form a Fabry-Perot cavity. A sketch of the system is

At time \(t = 0\), the electric potential \(V(t)\)
of the left electrode is suddenly raised from zero
to a finite value, which is taken into account by a
time-dependent coupling element (shown in red) between the left electrode and the central system.
We want to study the transient
regime of the current \(I(t)\) before it eventually reaches its
stationary value. This system has been studied in Ref. [1].
The actual simulation script in this tutorial is taken from Ref. [2],
but simulation time and accuracy are both reduced in this tutorial
in order to speed up the calculation. Note the method refine_intervals(),
which is used to adaptively refine the manybody integral.
In practice, both arguments rtol and atol must be set to smaller values,
or removed completely, to converge the result and to obtain numerically correct numbers.
The entire simulation script is:
from math import sin, pi import matplotlib.pyplot as plt import tkwant import kwant def am_master(): """Return true for the MPI master rank""" return tkwant.mpi.get_communicator().rank == 0 def make_fabry_perot_system(): # Define an empty tight-binding system on a square lattice. lat = kwant.lattice.square(norbs=1) syst = kwant.Builder() # Central scattering region. syst[(lat(x, 0) for x in range(80))] = 0 syst[lat.neighbors()] = -1 # Backgate potential. syst[(lat(x, 0) for x in range(5, 75))] = -0.0956 # Barrier potential. syst[[lat(4, 0), lat(75, 0)]] = 5.19615 # Attach lead on the left- and on the right-hand side. sym = kwant.TranslationalSymmetry((-1, 0)) lead = kwant.Builder(sym) lead[(lat(0, 0))] = 0 lead[lat.neighbors()] = -1 syst.attach_lead(lead) syst.attach_lead(lead.reversed()) return syst, lat # Phase from the time integrated voltage V(t). def phi(time): vb, tau = 0.6, 30. if time > tau: return vb * (time - tau / 2.) return vb / 2. * (time - tau / pi * sin(pi * time / tau)) def main(): times = range(220) # Make the system and add voltage V(t) to the left lead (index 0). syst, lat = make_fabry_perot_system() tkwant.leads.add_voltage(syst, 0, phi) syst = syst.finalized() # Define an operator to measure the current from site 77 to site 78 # on the right side after the barrier. hoppings = [(lat(78, 0), lat(77, 0))] current_operator = kwant.operator.Current(syst, where=hoppings) # Set occupation T = 0 and mu = -1 for both leads. occup = tkwant.manybody.lead_occupation(chemical_potential=-1) # Initialize the time-dependent manybody state. Here we use a lower # accuracy for the initial adaptive refinement (at time=0) to speed up the calculation. # For a realistic simulation, set rtol and atol to smaller values. state = tkwant.manybody.State(syst, tmax=max(times), occupations=occup, refine=False) state.refine_intervals(rtol=0.3, atol=0.3) # Loop over timesteps and evaluate the current. currents = [] for time in times: state.evolve(time) # For a realistic simulation, one must set rtol and atol to smaller values, # or remove both arguments completely, to converge the manybody integral. state.refine_intervals(rtol=0.3, atol=0.3) current = state.evaluate(current_operator) currents.append(current) # Plot the normalized current vs. time. if am_master(): plt.plot(times, currents / currents[-1]) plt.xlabel(r'time $t$') plt.ylabel(r'current $I$') plt.show() if __name__ == '__main__': main()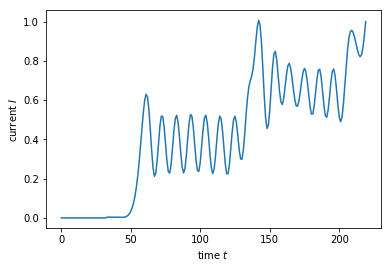
See also
The complete source code of this example can be found in
fabry_perot.py.
The result of the simulation shows the current increases through plateaus that correspond to the different trajectories of the cavity. The first plateau corrsponds to a direct transmission, whereas the second one is due to reflection at B followed by reflection at A then transmission. For longer simulation times, this series continues until a stationary current value is reached, see Refs. [1, 2]. Another detail is that on each plateau, the current oscillates with a frequency \(e V_b / h\), where \(V_b\) is the stationary value of the electric potential \(V(t)\).
Note
The examples in this section take several minutes on a single core desktop computer. To speed up the computation the script can be run in parallel, see section Parallelization with MPI.
2.3.1. References¶
[1] B. Gaury, J. Weston, X. Waintal, The a.c. Josephson effect without superconductivity, Nat. Commun. 6, 6524 (2015). [arXiv]
[2] T. Kloss, J. Weston, B. Gaury, B. Rossignol, C. Groth and X. Waintal, Tkwant: a software package for time-dependent quantum transport New J. Phys. 23, 023025 (2021), arXiv:2009.03132 [cond-mat.mes-hall].
