Evolution of an eigenstate of a finite 2D system subject to a time-dependent gate

Problem formulation

Evolving single-particle states forward in time in a closed system, and calculating the expectation value of the radial position operator. The Hamiltonian is

\[H(t) = \sum_{ij \in R} 4 \gamma |i,j \rangle \langle i,j | - e^{i B y_i} \gamma (|i+1,j \rangle \langle i,j | + \text{h.c.}) - \gamma (|i,j + 1 \rangle \langle i,j | + \text{h.c.}) + \sum_{ij \in R_t} r_{ij} V(t) \gamma |i,j \rangle \langle i,j |\]

with \(r_{ij} = \sqrt{x_i^2 + y_i^2}\), \(V(t) = V (1 - \cos(t))\), \(\gamma\) the hopping integral and B is the magnetic field strenght. The system is defined with a circular shape with radius R and \(R_t\) is some smaller circle inside (sites in red) where the time-dependent perturbation is applied.

We solve the eigenvalue problem

\[H(t=0) \psi_0 = E \psi_0\]

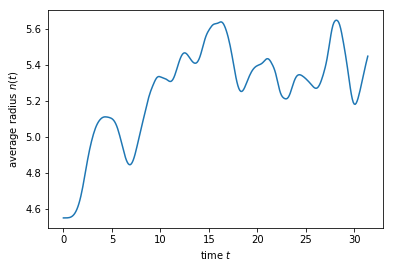
and evolve eigenstate with the lowest energy in time with initial condition \(\psi(t=0) = \psi_0\) with the time-dependent Schrödinger equation. The evolution of the radial density

\[n(t) = \sum_{i,j} r_{ij} \psi^*(t, x_i) \psi(t, x_j)\]

is plotted over time.

tkwant features highlighted

• Use of tkwant.onebody.WaveFunction to solve the time-dependent Schrödinger equation for a closed system.

from cmath import exp
from math import cos, sqrt, pi
import numpy as np
import matplotlib.pyplot as plt

import kwant
import tkwant


def make_system(a=1, gamma=1.0, radius=10, radius_time_dep=3):
    """Make a tight binding system on a single square lattice"""
    # `a` is the lattice constant and `gamma` the hopping integral
    # both set by default to 1 for simplicity.

    lat = kwant.lattice.square(a, norbs=1)
    syst = kwant.Builder()

    def circle(r):
        def inner(pos):
            (x, y) = pos
            return x ** 2 + y ** 2 < r ** 2
        return inner

    def hopx(site1, site2, magnetic_field_strength):
        y = site1.pos[1]
        return -gamma * exp(-1j * magnetic_field_strength * y)

    def potential(site, time, voltage):
        x, y = site.pos
        return 4 * gamma + sqrt(x**2 + y**2) * voltage * (1 - cos(time))

    def side_color_func(site):
            time_dep = circle(radius_time_dep)
            return 'r' if time_dep(site.pos) else 'k'

    # Define the quantum dot
    syst[lat.shape(circle(radius), (0, 0))] = 4 * gamma
    syst[lat.shape(circle(radius_time_dep), (0, 0))] = potential
    # hoppings in x-direction
    syst[kwant.builder.HoppingKind((1, 0), lat, lat)] = hopx
    # hoppings in y-directions
    syst[kwant.builder.HoppingKind((0, 1), lat, lat)] = -gamma

    # Plot system
    kwant.plot(syst, site_color=side_color_func)

    # It's a closed system, so no leads
    return syst


def main():

    # construct a tight binding system and plot it
    syst = make_system().finalized()

    # set parameters
    params = {'voltage': 1.0, 'magnetic_field_strength': 1.0}

    tparams = params.copy()
    tparams['time'] = 0  # the initial time

    # create an observable for calculating the average radius of a wavefunction
    def radius(site):
        x, y = site.pos
        return sqrt(x**2 + y**2)

    density_operator = kwant.operator.Density(syst, radius, sum=True)

    # create a time-dependent wavefunction that starts in the ground state
    hamiltonian = syst.hamiltonian_submatrix(params=tparams)
    eigenvalues, eigenvectors = np.linalg.eigh(hamiltonian)

    ground_state = tkwant.onebody.WaveFunction.from_kwant(syst=syst,
                                                          psi_init=eigenvectors[:, 0],
                                                          energy=eigenvalues[0],
                                                          params=params)

    # evolve forward in time, calculating the average radius of the wavefunction
    times = np.arange(0, 10 * pi, 0.1)
    average_radius = []
    for time in times:
        ground_state.evolve(time)
        density = ground_state.evaluate(density_operator)
        average_radius.append(density)

    # plot the result
    plt.plot(times, average_radius)
    plt.xlabel(r'time $t$')
    plt.ylabel(r'average radius $n(t)$')
    plt.show()


if __name__ == '__main__':
    main()

See also

The complete source code of this example can be found in closed_system.py.